之前讲了下梯度下降法对波士顿房价进行预测,当时的特征变量只有1个,就是房间数对房价的影响,而数据集变量有13个,单纯挑出一个变量进行建模不够准确,那么,拓展到n个变量,对于n个特征变量我们如何求解呢,如下所示数据集样例
x1,x2,x3,x4为特征变量(从3个变量中抽取4个典型),y为特征标签,数据集样本506个,我们的假设函数(线性函数)则为H(x) = O_0+O_1*x1+O_2*x+O_3*x+O_4*x,同样的,我们的目的是求O_0,O_1,O_2和O_3参数,我们再看下损失函数,可以和之前一元的对比下,并进行递推过程如下所示

将获得的公式代入损失函数得

明白了矩阵的用法,我们可以来求多元函数变量了,为了画图直观,这里选择2元假设函数,方便我们画3维图进行可视化展示,我们这里选择房间数和便利指数2个变量进行房价预测,由于这2个变量数据相差较大,会可能产生较大的问题,如图
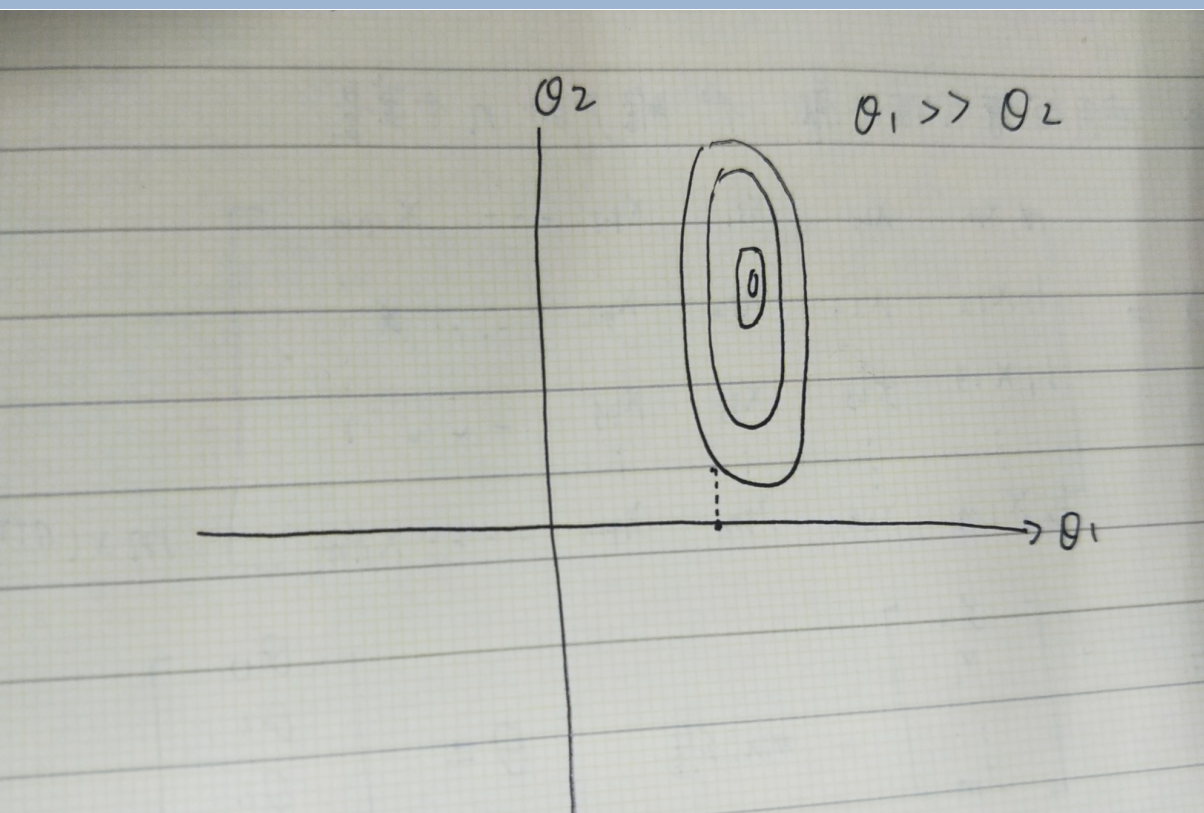
假设O1远远大于O2,则呈现的俯视图可能是椭圆的,因为最后结果基本受O1的控制,对于梯度下降很不友好的,因此我们对其进行线性归一化处理,代码如下所示
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import time
#设置防止中文乱码
plt.rcParams['font.sans-serif']=[u'SimHei']
plt.rcParams['axes.unicode_minus']=False
#载入数据,并进行读取
data = pd.read_csv('C:/users/14499/desktop/housing.data')
def notEmpty(s):
return s!=''
#创建len(data)行,14列的空二维数组(矩阵)
df = np.empty((len(data), 14))
#迭代所有数据
for i, d in enumerate(data.values):
#先使用filter去掉为空的字符串,然后将字符串分割成列表,并将列表元素转化为浮点型
m = map(float, filter(notEmpty, d[0].split(' ')))
#将这行数据存入二维数组的第i整行
df[i] = list(m)
names = ['CRIM','ZN', 'INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
#设置列名,将原来的二维数组转化为代标签的二维数组,方便以列名进行存取
df1 = pd.DataFrame(df,columns=names)
#取房间个数数据
room_num = df1['RM']
#距离高速公路的便利指数
convenient = df1['RAD']
#取价格数据
price_num = df1['MEDV']
x0 = np.ones(len(room_num))
#对房间数进行归一化处理
x1 = (room_num-room_num.min())/(room_num.max()-room_num.min())
print(x1)
#对便利指数进行归一化处理
x2 = (convenient-convenient.min())/(convenient.max()-convenient.min())
m = len(x2)
print(list(x2))
print('x2',x2)
X = np.stack((x0,x1,x2),axis=1)
#转化为列向量
Y = np.array(price_num).reshape(-1,1)
print(X)
print(Y)
a = 0.001
Theata = np.random.randn(3,1)
for i in range(100):
Theata = Theata - a*np.matmul(np.transpose(X),np.matmul(X,Theata)-Y)
H = np.matmul(X,Theata)
loss = np.mean(np.square(Y-H))/2
print('loss:{} O参数:{}'.format(loss,Theata))
# print(H)
# print(Theata)
fig=plt.figure()
ax=Axes3D(fig)
ax.scatter(x1,x2,price_num,c='green')
ax.set_xlabel('房间数(归一化后)') # 画出坐标轴
ax.set_ylabel('便利指数')
ax.set_zlabel('价格')
ax.plot_trisurf(x1,x2,H.reshape(-1),cmap="viridis")
plt.show()
最后拟合的图像如图所示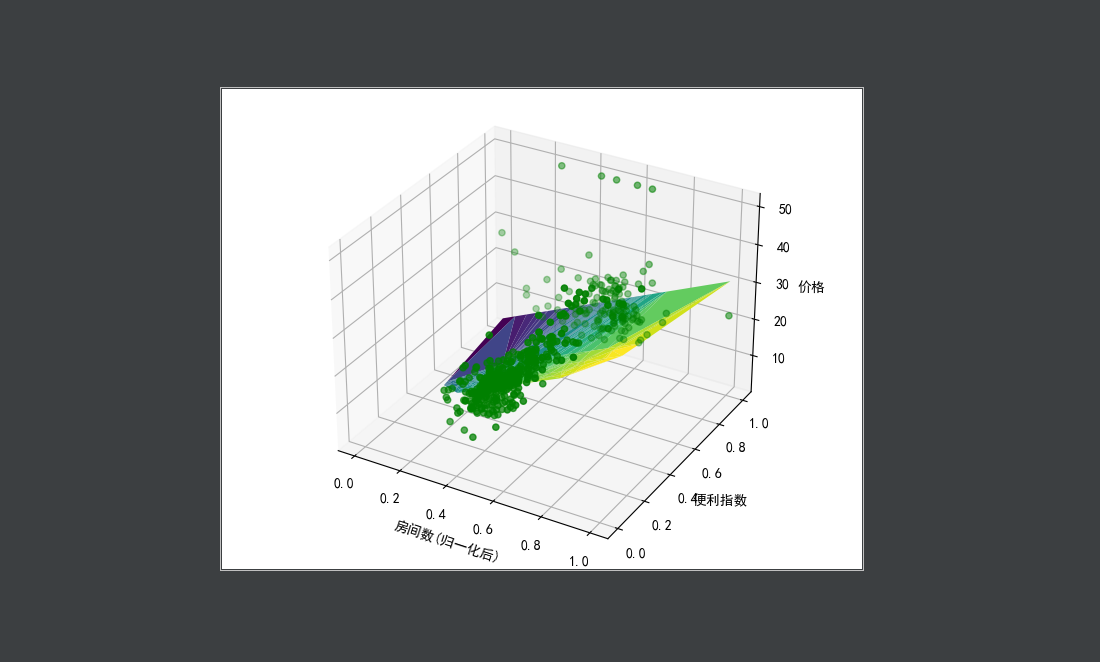
二维是一个直线,3维的假设函数就是一个面了,四维以上的图像就画不出来了,这里以3维为例子,损失结果如图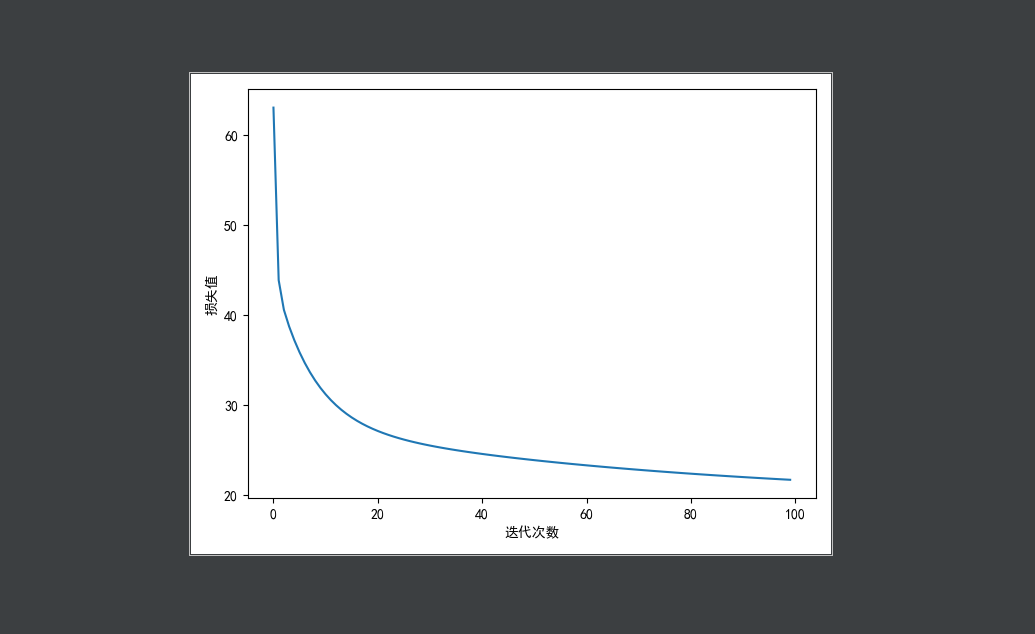
如果上述代码帮助您很多,可以打赏下以减少服务器的开支吗,万分感谢!


 赣公网安备 36092402000079号
赣公网安备 36092402000079号
点击此处登录后即可评论